Deep Unsupervised Learning using Nonequilibrium Thermodynamics
Abstract
머신러닝에서는 많은 데이터들을 통해 예측 모델을 만들게 되는데 이때 얼마나 유연하게(flexibility) 데이터에 맞추는지와 다루기 쉬운지(tractability)가 중요하다.
non-equilibrium statistical physics에서 영감을 받아서 generative 모델을 만들었다.
천천히 체계적으로 데이터의 분포를 파괴한뒤 (forward diffusion process) 복구 하면 복구하는 과정을 통해서 유연하고 다루기 쉬운 생성 모델을 만들 수 있다.
Intorduction
다루기 쉬운 모델은 분석적으로 평가할 수 있고 쉽게 데이터에 모델을 맞출 수 있지만 거대한 데이터셋에서는 맞추기 어려운 점이 있다. 유연한 모델은 반대로 데이터 구조에 맞게 변경할 수 있다.
non-negative function 인 $\phi(x)$가 있을때 분포 $p(x) = { {\phi(x)} \over {Z} }$ , ($Z$는 normalization constant)가 있다고 하자. 이는 데이터 구조에 맞게 분포를 설명할 수 있지만 $Z$를 구하는 것은 어렵다(intractable).
여기서 정규화 상수는 $\phi(x)$ 의 적분값이 1이 되게 하는 상수이다.
diffusion probabilistic models
논문에서 제안하는 예측 모델을 정의하는 새로운 방법은
- 모델 구조가 유연하다.
- 정확하게 표본을 추출할 수 있다.
- 다른 분포와의 multiplication이 쉽다. (posterior probability등, inpainting 이나 denoising에 사용될 수 있음)
- 모델이 log-likelihood이고 개별 상태를 평가하는데 비용이 적다(likelihood 함수는 직관적이고 관측결과로 쉽게 계산이 가능하다).
앞서 말했듯 논문에서는 차례적으로 분포를 파괴하는 단계를 거치는데 이때 마르코프 체인을 활용하게 된다. 따라서 단계별로 확률적으로 해석할 수 있고 분석 평가가 가능하다.
Algorithm
목적은 어떠한 복잡한 분포를 가지고 있는 데이터를 forward diffusion process를 통해서 간단하고 다루기 쉬운 분포로 변환하고 반대 과정의 reverse diffusion process를 학습하여 이를 generative model로 이용한다.
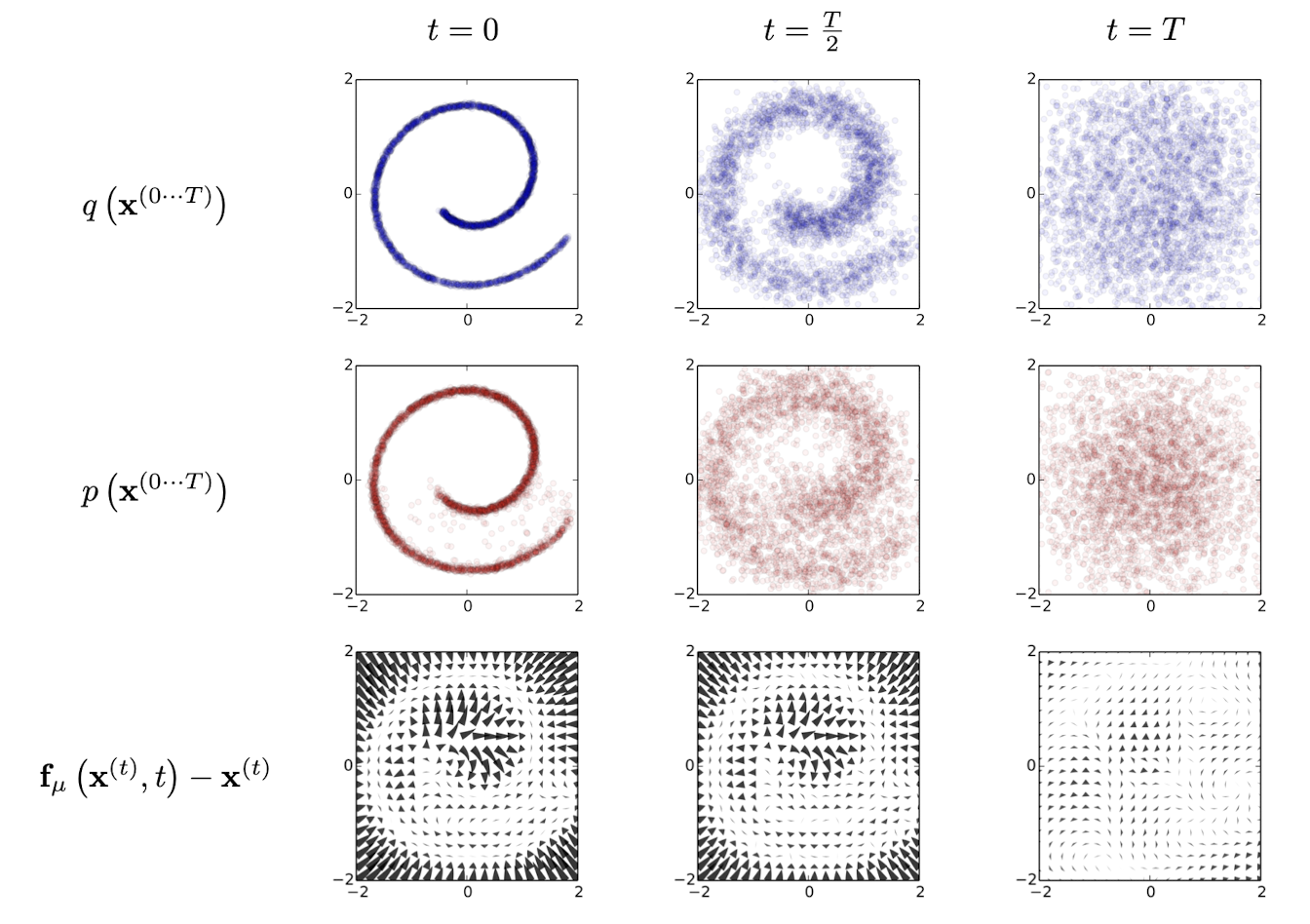
위 이미지는 논문에서 제안된 모델링 방법으로 2-d swiss roll data에 학습된 결과를 보여준다.
첫번째 행(foward trajectory $q(\mathbf{x}^{(0\cdots T)})$)을 보면 시간에 따라서 데이터의 분포가 gaussian diffusion에 따라서 Identity-covariance gaussian 분포로 점진적으로 변하게 된다. (여기서 Identity-convariance는 모든 차원이 독립적이고 각 차원에 데한 데이터의 분산이 1인 경우를 의미한다.[8])
두번째 행(reverse trajectory $p(\mathbf{x}^{(0\cdots T)})$)를 보면 학습된 평균, 분산 함수에 의해서 Identity-covariance gaussian 분포에서 gaussian diffusion 프로세스로 원본 데이터로 복구되는 모습을 볼 수 있다.
마지막 행은 reverse diffusion이 어떻게 이동하는지에 대한 모습을 보여준다. ($f_\mu (\mathbf{x}^{(t)},t) - \mathbf{x}^{(t)}$ 로 표현되는데 여기서 $f_\mu$는 $t$에서 $\mathbf{x}^{(t)}$의 reverse diffusion을 의미하는것 같다.)
Forward Trajectory
Forwardf Trajectory의 수식은 다음과 같다.
\[\begin{align} \pi(\mathbf{y}) &= \int{d\mathbf{y}'T_\pi(\mathbf{y}|\mathbf{y}';\beta) \pi(\mathbf{y}')} \\ q(\mathbf{x^{(t)}|\mathbf{x}^{(t-1)}}) &= T_\pi (\mathbf{x^{(t)}|\mathbf{x}^{(t-1)}} ; \beta_t) \end{align}\]
마르코프 diffusiond kernal $T_\pi(\mathbf{x^{(t)}}|\mathbf{y^{(t-1)}};\beta_t)$ 를 이용해서 이전 시간으로부터 현재 분포 $q(\mathbf{x^{(t)}|\mathbf{x}^{(t-1)}})$를 구하고 마르코프 체인을 유한한 시간내에서 반복하면 다루기 쉬운 분포로 이루어진 $\pi(\mathbf{y})$를 구할 수 있다.
원 데이터의 분포가 $q(\mathbf{x}^{(x)})$라고 하면 forward trajectory는 아래처럼 표현 가능하다.
\[q(\mathbf{x}^{(0\cdots T)}) = q(\mathbf{x}^{(0)})\prod_{t=1}^{T} q(\mathbf{x^{(t)}|\mathbf{x}^{(t-1)}})\]
이때 반복해서 곱해지는 분포 $q(\mathbf{x^{(t)}|\mathbf{x}^{(t-1)}})$는 Identity-convariance Gaussian 분포나 binominal(아래의 내용에서 언급은 잘 안할것 같다. 주로 gaussian 위주로 볼듯 하다) distribution이 사용된다. 실제 논문에서 사용된 분포는 다음과 같다.
Reverse Trajectory
생성 분포는 (역과정은 결국 분포를 생성하는 과정이므로 이렇게 표현하는것 같다.) 같은 trajectory를 따라가지만 반대로 적용된다.
\[\begin{align} p(\mathbf{x}^{(T)}) &= \pi(\mathbf{x}^{(T)}) \\ p(\mathbf{x}^{(0\cdots T)}) &= p(\mathbf{x}^{(T)})\prod_{t=1}^{T} p(\mathbf{x^{(t-1)}|\mathbf{x}^{(t)}}) \end{align}\]
이처럼 반대로의 확산도 하나의 스텝이 작다($\beta$의 사이즈)는 가정하에 동일한 형태를 가지고 있다고 한다[9]. 따라서 $q(\mathbf{x^{(t)}|\mathbf{x}^{(t-1)}})$가 gaussian이나 binominal 분포이면서 그 스텝인 $\beta_t$가 작다면 $q(\mathbf{x^{(t-1)}|\mathbf{x}^{(t)}})$ 또한 가우시안 또는 이산 분포가 된다.
따라서 스텝이 길어지고 $\beta$ 가 작아진다면 쉽게 역변환을 할 수 있다.
이때 가우시안 분포는 평균과 분산만 있다면 구할 수 있기때문에 이과정에서 평균과 분산을 학습시키면 역과정, 즉 분포를 생성하는 모델(generative model)을 구성할 수 있다.
이제 가우시안 분포를 이용한다고 가정하면 위에서 본 표를 살펴보면 Reverse diffusion kernel은 다음과 같이 정의된다.
\[p(\mathbf{x^{(t-1)}|\mathbf{x}^{(t)}}) = \mathcal{N}(\mathbf{x^{(t-1)}};\mathbf{f}_\mu(\mathbf{x^{(t)}, t}), \mathbf{f}_\Sigma(\mathbf{x^{(t)}, t}))\]
즉 학습해야 되는 요소는 각 스텝별 \(\mathbf{f}_\mu(\mathbf{x^{(t)}, t})\), \(\mathbf{f}_\Sigma(\mathbf{x^{(t)}, t})\) 와 얼마나 많은 스텝$\beta_t$이 적용되는가만 구하면 된다.
논문에서는 이 함수를 정의하기 위해서 MLP를 적용하였다.
Model probability
이제 reverser trajectory의 방법을 통해서 원 분포인 $p(\mathbf{x}^{(0)})$를 찾아보자.
원분포는 다음과 같이 표현할 수 있다.
\[p(\mathbf{x}^{(0)}) = \int{d\mathbf{x}^{(1 \cdots T)} p(\mathbf{x}^{(0 \cdots T)})}\]내 예상으로 저렇게 표현되는 이유는 앞서 forward trajectory에서 최종적으로 tractable한 분포로 변환하는 과정을 수식 (1)과 같이 표현하였다. \(\pi(\mathbf{y}) = \int{d\mathbf{y}'T_\pi(\mathbf{y}|\mathbf{y}';\beta) \pi(\mathbf{y}')} \nonumber\)
reverse trajectory로 동일한 분포를 이용하므로 반대로 최종 분포를 $p(\mathbf{x}^{(0)})$로 하면
\[\begin{align} p(\mathbf{x}^{(0)}) &= \int{dp(\mathbf{x}^{T})\mathbf{x}^{(1 \cdots T)} p(\mathbf{x}^{(0 \cdots T-1)})} \\ &= \int{d\mathbf{x}^{(1 \cdots T)} p(\mathbf{x}^{(0 \cdots T)})} \end{align}\]처럼 표현된게 아닐까 싶다.
이때 $p(\mathbf{x}^{(0)})$는 매스텝의 reverse 전이확률과 스텝의 길이등을 알아야해서 intractable 하다. 이때 annealed importance sampling 과 Jarzynski equality를 이용하면 아래처럼 정리할 수 있다고 한다.
\[\begin{align} p(\mathbf{x}^{(0)}) &= \int{d\mathbf{x}^{(1 \cdots T)} p(\mathbf{x}^{(0 \cdots T)})} { { q(\mathbf{x}^{(1\cdots T)}|\mathbf{x}^{(0)}) }\over{q(\mathbf{x}^{(1\cdots T)}|\mathbf{x}^{(0) }) } } \\ &= \int{d\mathbf{x}^{(1 \cdots T)} q(\mathbf{x}^{(1\cdots T)}|\mathbf{x}^{(0)})} { {p(\mathbf{x}^{(0 \cdots T)})}\over{q(\mathbf{x}^{(1\cdots T)}|\mathbf{x}^{(0)}) }} \\ &= \int{d\mathbf{x}^{(1 \cdots T)} q(\mathbf{x}^{(1\cdots T)}|\mathbf{x}^{(0)})} \cdot p(\mathbf{x}^{(T)})\prod_{t=1}^{T} { {p(\mathbf{x^{(t-1)}|\mathbf{x}^{(t)}})}\over{q(\mathbf{x^{(t)}|\mathbf{x}^{(t-1)}})}} \end{align}\]
이때 앞서 설명했듯 $\beta$가 작다면 forward, reverse의 분포는 같아지고 다음 수식과 같아진다.
이 적분을 풀기위해서는 forward의 $q(\mathbf{x}^{(1\cdots T)}|\mathbf{x}^{(0)})$ 샘플만 가지고 있으면 된다. (즉 tractable 하다.)
Training
여기서 구하고자 하는 p(를 구하기 위해서 다음과 같이 maximum log-likelihood estimation을 적용할 수 있다. 이때 $q( \mathbf{x}^{(0)})$는 forward trajectory로 알 수 있고 $p( \mathbf{x}^{(0)})$는 구해야할 reverse trajectory 이다.
\[\begin{align} L &= \int d \mathbf{x}^{(0)}q( \mathbf{x}^{(0)}) \mathbf p( \mathbf{x}^{(0)}) \\ &= \int d \mathbf{x}^{(0)}q( \mathbf{x}^{(0)}) \cdot \mathbf{log} \left[\int{d\mathbf{x}^{(1 \cdots T)} q(\mathbf{x}^{(1\cdots T)}|\mathbf{x}^{(0)})} \cdot p(\mathbf{x}^{(T)})\prod_{t=1}^{T} { {p(\mathbf{x^{(t-1)}|\mathbf{x}^{(t)}})}\over{ q(\mathbf{x^{(t)}|\mathbf{x}^{(t-1)}})}}\right] \end{align}\]
이때 Jensen’s inequality에 의해서 아래와 같은 lower bound를 가지게 된다. 여기서 엔트로피와 KL divergence는 계산이 가능하다. (논문의 Appendix.B에 정리한 내용을 볼 수 있다. $H()$는 엔트로피를 의미한다.)
여기서 만약 forward와 reverse trajectory 가 같아진다면 (즉, $\beta$ 가 작다면) 위식은 $L=K$ 가 된다.
이를 정리하면 reverse Markov transition들을 모두 찾는 것은 (가우시안의 경우 mean, variance를 찾는것) log-likelihood의 lower bound를 maximize 하는 것과 같다. 즉,
\[\DeclareMathOperator*{\argmax}{argmax} \hat p (\mathbf{x}^{(t-1)}|\mathbf{x}^{(t)}) = \argmax_{ p (\mathbf{x}^{(t-1)}|\mathbf{x}^{(t)})} K\]Setting the diffusion rate $\beta_{t}$
앞서 말한것 처럼 forward trajectory에서 diffusion schedule이라고 할 수 있는 $\beta_{t}$를 결정하는 것은 성능에 크게 영향을 미친다 (annealed importance sampling (AIS) 나 thermodynamics에서도 스케줄은 중요하다고 한다.). 논문에서는 gaussian diffusion에서는 forward diffusion schedule $\beta_{2 \cdots T}$를 $K$에 gradient ascent를 적용해서 학습시킨다고 한다.
$\beta_1$은 오버피팅 방지를 위해서 첫 스텝에 작은 상수를 넣어준다.
\(q( \mathbf{x}^{(1 \cdots T)} | \mathbf{x}^{(0)} )\) 부터 $\beta_{1 \cdots T}$로 의존성은 VAE 논문의 frozen-noise를 이용해서 명시된다.
(VAE 논문에서 reparameterization trick 에서 나오는 auxiliary noise 를 말하는것 같다. VAE에서는 decoder에 latent variable $z$를 넣어야하고 아를 위해서는 그 수만큼 샘플링을 해야는데 이때 sampling을 하는 과정은 미분이 불가하다(즉 gardient 계산 불가). reparameterization trick은 간단하게 확률적으로 정의될 수 있는 값(분포로 설명되는 가우시안과 같은)을 미분이 가능한 deterministic 부분과 확률적인 stochastic 부분으로 나눠서 미분이 가능한 deterministic 부분의 항을 통해서 backpropagation을 전달하는 방법이다.
예를 들어 auxiliary noise $\epsilon \sim \mathcal{N}(0, 1)$을 이용해서 $\epsilon \sim \mathcal{N}(\mu_{\phi}, \sigma^2_{\phi})$ 분포를 두 부분으로 다음과 같이 표현할 수 있다.
\[x = g(\phi, \epsilon)= \mu_{\phi} + \sigma^2_{\phi} \cdot \epsilon\]이러면 $\mu_{\phi}$ 를 통해서 gardient를 구할 수 있다.
이부분은 좀 더 생각을 해봐야하는데 확률($K$)로부터의 gradient를 활용해 구해야해서 VAE와 같은 트릭을 활용한게 아닌가 싶다. (코드를 살펴봐야겠다.)
Multiplying distributions, and computing posteriors
Denoising이나 빠진 부분을 추론하기 위해서 posterior를 구하는 경우 새로운 분포$\tilde{p}(\mathbf{x}^{(0)})$를 만들어야 하기 때문에 모델의 분포$p(\mathbf{x}^{(0)})$와 다른 분포(secondary distribution)$r(\mathbf{x}^{(0)})$를 곱할 수 있어야 한다.
\[\tilde{p}(\mathbf{x}^{(0)}) \propto p(\mathbf{x}^{(0)})r(\mathbf{x}^{(0)})\]일반적으로 분포간의 곱은 계산이 매우 복잡한데 본 논문에서는 secondary distribution을 각 diffusion 단계의 작은 노이즈처럼 다룬다. 그럼 아래의 사진처럼 결과를 얻을 수 있다.
Modified marginal distributions
위에서 언급한 새로 만들어진 분포 $\tilde{p}(\mathbf{x}^{(0)})$ 또한 확률 분포가 되어야해서 아래와 같이 normalizing constant $\tilde{Z_t}$를 이용해서 새로운 분포를 확률 분포로 만들어준다. 또한 아래의 수식에서 보듯 각 reverse trajectory 스텝$t$ 마다 secondary distribution $r(\mathbf{x}^{(t)})$ 가 곱해지는것을 볼 수 있다.
\[\tilde{p}(\mathbf{x}^{(t)}) = { {1}\over{\tilde{Z_t}}}p(\mathbf{x}^{(t)})r(\mathbf{x}^{(t)})\]Modified diffusion steps
앞서 위에서 보았던 수식을 정리하면 reverse diffusion의 마르코프 커널은 다음식처럼 표현이 가능하다.
\[p(x^{(t)}) = \int{d\mathbf{x}^{(t+1)} p(\mathbf{x}^{(t)}|\mathbf{x}^{(t+1)})} \cdot p(\mathbf{x}^{(t+1)})\]
이를 새로 만들어진 분포에 적용하면, \(\begin{align} \tilde{p}(x^{(t)}) &= \int{d\mathbf{x}^{(t+1)} \tilde{p}(\mathbf{x}^{(t)}|\mathbf{x}^{(t+1)})} \cdot \tilde{p}(\mathbf{x}^{(t+1)}) \\ { {1}\over{\tilde{Z_t}}}p(\mathbf{x}^{(t)})r(\mathbf{x}^{(t)}) &= \int{d\mathbf{x}^{(t+1)} \tilde{p}(\mathbf{x}^{(t)}|\mathbf{x}^{(t+1)})} \cdot { {1}\over{\tilde{Z}_{t+1}}}p(\mathbf{x}^{(t+1)})r(\mathbf{x}^{(t+1)}) \\ \end{align}\)
이때 ,
을 만족하면, 앞선 식은 다음과 같이 표현된다.
이때 이 분포가 normalize된 확률 분포 형태로 만들기 위해서 아래와 같이 만들 수 있는 확률$\tilde{p}(\mathbf{x}^{(t)}|\mathbf{x}^{(t+1)})$를 정의한다.
각 diffusion step에서 $r( \mathbf{x}^{(t)} )$은 작은 분산으로 인해 급격한 값을 가지게 되고, 이를 보면 ${r( \mathbf{x}^{(t)} )}\over{r( \mathbf{x}^{(t+1)} )}$ 은 작은 노이즈 정도로 여겨질 수 있다고 한다. (아무래도 큰값들 사이의 변화정도라서 작은 노이즈 정도로 볼 수 있는것 같다.)
여기서 \(r(\mathbf{x}^{(t)})\) 가 smooth한 분포를 가지면 노이즈 정도로 여길수 있고 \(\tilde{p}(\mathbf{x}^{(t)} | \mathbf{x}^{(t+1)})\)과 \({p}(\mathbf{x}^{(t)}|\mathbf{x}^{(t+1)})\)는 같은 형태를 가지게 된다. (smooth의 기준이 uniform distribution에 가까운 분포의 형태를 말하는것 같다. 변화가 적은?)
이때 $r(\mathbf{x}^{(t)})$는 각 step에 따라서 천천히 변해야 하는데, 논문에서는 그냥 상수를 사용해버렸다.
Entropy of reverse process
forward trajectory process를 알고 있기때문에 각 단계의 conditional entroy 를 구할 수 있는데 그 수식은 다음과 같이 표현된다고 한다.
\[\begin{align} H_q(X^{(t)}|X^{(t+1)}) + H_q(X^{(t-1)}|X^{(0)}) - H_q(X^{(t)}|X^{(0)}) &\le H_q(X^{(t-1)}|X^{(t)}) \\ H_q(X^{(t-1)}|X^{(t)}) &\le H_q(X^{(t)}|X^{(t-1)}) \end{align}\]Experiments
Appendix
log-likelihood
딥러닝에서 weight $w$ 를 구하는 log-likelihood는 다음과 같이 표현할 수 있다.
\[\hat{w} = \mathbf{argmax}\sum_{i=1}^{N}\mathbf{log}P(y_i|x_i; w)\]
이 수식을 negative하게 바꾸면,
cross-entropy를 목적함수로 사용한다고 하면 수식은 다음과 같다.
이를 딥러닝 모델에 적용해보면,
이때 $P(y_i|x_i)$는 우리가 알고 있는 답, (0, 1) 이므로 실제로 $-\sum_{i=1}^{N}\mathbf{log}P(y_i|x_i; w) (P(y_i|x_i)\neq0)$만 남는다. 즉 이는 cross-entropy를 목적함수로 사용하면 결국 음의 로그우도를 최소화, 즉 로그우도를 최대화 하는것과 같다는 의미이다.
따라서 일반적인 딥러닝 학습에 maximum log-likelihood(최대 우도법)를 적용한다고 볼 수 있다.
Bayes’ theorem
\(P(A|B) = { {P(B|A)\cdot P(A)} \over {P(B)}}\) 일때 조건부 확률 $P(B|A)$는 Likelihood (A가 참일때 B의 확률), \(P(A)\)는 Prior(이미 알고 있는 A 확률), \(P(A|B)\)는 Posterior.
이 posterior가 ML과 관련이 깊은 이유는 학습데이터의 분포가 $D$, 구하고자 하는 모델(weight)$P(W|D)$라고 한다면 \(P(W|D) = { {P(D|W)\cdot P(W)} \over {P(D)}}\)로 표현 가능하다. Maximum Likelihood Estimation(MLE)는 \(P(D|W)\)를 최대화 하는 \(W\)를 찾는것.
Markov chain
마르코프 체인은 각 전 상태가 현재의 상태에 영향을 미치는 성질을 이용한 과정을 예기한다. 예를들어서 오늘 비가 올 확률과 같은 경우이다.
n차 마르코프 체인은 상태 전이 확률(State transition Probability) \(P(o_t|o_{t-1}o_{t-2}..{o_1})\) 로 나타낼 수 있고 아래 그림처럼 표현할 수 있다.
graph LR
subgraph 2차 마르코프 체인
E(O1)
F(O2)
G(O3)
H(On-2)
I(On-1)
J(On)
E --> F
E --> G
F --> G
G -.-> H
H -->I
H -->J
I --> J
end
subgraph 1차 마르코프 체인
A(O1)
B(O2)
C(O3)
D(On)
A --> B
B --> C
C -.-> D
end
날씨에 마르코프 체인 적용해보기
오늘 날씨($o_{t-1}$)에 대한 내일 날씨($o_t$)의 확률이 다음과 같을때,
| 오늘 날씨 \ 내일 날씨 | 맑음 | 흐림 |
|---|---|---|
| 맑음 | 0.8 | 0.2 |
| 흐림 | 0.3 | 0.5 |
마르코프 상태 전이도는 다음과 같이 표현된다.
flowchart LR
A[맑음]
B[흐림]
A -->|0.5| A
A -->|0.2| B
B -->|0.3| A
B -->|0.8| B
이 전이확률을 행렬로 표현하면 다음과 같다.
\[P = \left[ \begin{array}{cc} 0.8 & 0.2 \\ 0.3 & 0.5 \\ \end{array} \right]\]
1차 마르코프 체인에 의해서 모레의 날씨 상태 전이행렬은,
| 오늘 날씨 \ 모레 날씨 | 맑음 | 흐림 |
|---|---|---|
| 맑음 | 0.7 | 0.26 |
| 흐림 | 0.39 | 0.31 |
로 나타낼 수 있다.
만약 오늘날씨가 맑을 확률이 90%일때 모레의 맑을 확률은,
$0.9$(오늘 맑을 확률)$\cdot 0.7 + 0.1$(오늘 흐릴 확률)$ \cdot 0.39 = 0.669$, 약 67% 확률이 나온다.
Reference
[1] https://blog.naver.com/reach0sea/222932879550
[2] https://en.wikipedia.org/wiki/Likelihood_function
[3] https://bioinformaticsandme.tistory.com/47
[4] https://towardsdatascience.com/bayesian-updating-in-python-8bbd0e7e30cc
[5] https://angeloyeo.github.io/2020/07/17/MLE.html
[6] https://www.puzzledata.com/blog190423/
[7] https://sites.google.com/site/machlearnwiki/RBM/markov-chain
[8] https://theclevermachine.wordpress.com/tag/identity-covariance/
[9] Feller, W. On the theory of stochastic processes, with par- ticular reference to applications. In Proceedings of the [First] Berkeley Symposium on Mathematical Statistics and Probability. The Regents of the University of Cali- fornia, 1949.
[10] https://ratsgo.github.io/deep%20learning/2017/09/24/loss/
[11] https://hulk89.github.io/machine%20learning/2017/11/20/reparametrization-trick/